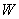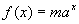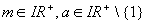Bestimme die Wertemenge der Exponentialfunktion () mit !    Hast du hier Probleme, lies in der allgemeinen Definition einer Funktion über die Wertemenge nach.

Die Wertemenge der Exponentialfunktion mi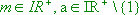t ist .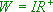

Falls du in GeoGebra etwas verändert hast, stelle rechts oben mit dem -Logo die Ausgangsposition wieder her.
Bewege nun den Schieberegler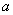 und notiere möglichst (mathematisch) exakt die Eigenschaften der Exponentialfunktion für 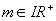hinsichtlich der Monotonie! (Fallunterscheidung)    Definition Monotonie

 Es gilt:
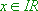-   : Der Graph ist für streng monoton steigend.
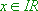-   : Der Graph ist für streng monoton fallend.

Gibt es einen Punkt, durch den die Funktionsschar bei festem verläuft?

Bei festem verläuft die Funktionsschar durch den Punkt .

Ziehe am Schieberegler 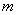und betrachte das Funktionsverhalten von 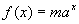(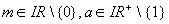) . Was kann an 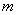abgelesen werden? (Fallunterscheidung)    Bei Unklarheiten schaue dir diesen Parameter bei den quadratischen Funktionen an.

An können folgende Eigenschaften abgelesen werden:
-   : Streckung des Graphen in Richtung der y-Achse.
-   : Stauchung des Graphen in Richtung der y-Achse.
-   : Zusätzliche Spiegelung von 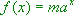(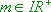) an der x-Achse.