Funktionsterm (Herleitung 2)

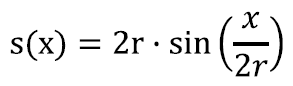
Der Sinus eines Winkels φ im rechtwinkligen Dreieck ist als Quotient aus Gegenkathete und Hypotenuse definiert. Zunächst müssen den Variablen in der Gleichung die richtigen Größen zugeordnet werden. φ ist hier der halbe Mittelpunktswinkel, also α/2, die Gegenkathete ist die Hälfte der Sehne s und die Hypotenuse ist der Radius r des Kreises. Einsetzen liefert: Auflösen nach s liefert: Daraus folgt mit α = x/r (Hilfe zu Winkeln im Bogenmaß: Bogenmaß):