Das Ziel lautet, die Abmessungen der oberflächenminimalen Konservendose bei einem festen Volumen von 916 ml (mit Hilfe der Differenzialrechnung) zu bestimmen.
Um dich mit der Aufgabe vertraut zu machen, kannst du dich mit GeoGebra beschäftigen.
-
Die nun folgenden Zwischenschritte sollen eine Hilfe beim Finden des optimalen Radius sein. Wenn du sie nicht benötigst, überspringe diese und prüfe lediglich dein Endergebnis nach oder versuche dich an Stufe 2.
- Wie findet man nun das Oberflächenminimum?
 Denke daran, dass die Ableitung in einem Punkt die dortige lokale Änderungsrate der Funktion angibt. Was muss also an einem Extremum gelten?
Denke daran, dass die Ableitung in einem Punkt die dortige lokale Änderungsrate der Funktion angibt. Was muss also an einem Extremum gelten?

Falls an einer (inneren) Stelle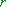 der Definitionsmenge ein Extremum vorliegt, so muss dort gelten:
der Definitionsmenge ein Extremum vorliegt, so muss dort gelten: 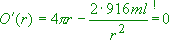
Durch Auflösen nach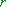 ergibt sich die einzige Nullstelle zu:
ergibt sich die einzige Nullstelle zu: 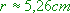 .
.
Für den Nachweis, dass tatsächlich ein Minimum existiert, kann die Eigenschaft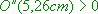 benutzt werden. (Warum?)
benutzt werden. (Warum?)
- Wie lauten also die Abmessungen der oberflächenminimalen Dose mit 916 ml Inhalt?

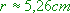 ,
, 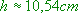
- Ziehe den Schieberegler
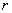 ungefähr auf das Ergebnis und betrachte das Bild der Dose. Klicke dann rechts oben auf das
ungefähr auf das Ergebnis und betrachte das Bild der Dose. Klicke dann rechts oben auf das  -Logo
und stelle damit die Realabmessungen der Dose her.
Was fällt dir im Vergleich auf?
-Logo
und stelle damit die Realabmessungen der Dose her.
Was fällt dir im Vergleich auf?

Die Abmessungen der oberflächenminimalen Dose entsprechen nicht denen der realen Dose.
- Überlege dir, warum dein Ergebnis für die Dosenabmessungen vom Hersteller nicht für diese Dose verwendet wird. Betrachte die Situation aus unterschiedlichen Perspektiven!

Der Hersteller muss viele weitere Gegebenheiten berücksichtigen, wie z. B.:
- Überstände an Boden, Deckel und Mantel (siehe Stufe 2)
- Verschnitt beim Zuschneiden der einzelnen Dosenteile
- Wegen der Stabilität sind Boden und Deckel häufig dicker.
- Ringförmige Ausbuchtungen des Mantels (sog. Sicken)
- Dosenhersteller sind an Normen gebunden, die oft nicht mit dem berechneten Optimum übereinstimmen.
- Marketinggesichtspunkte, z. B. soll die Werbebotschaft des Herstellers optimal auf der Dose sichtbar sein.
- ...
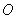 , ausgedrückt als Funktion des Radius
, ausgedrückt als Funktion des Radius 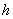 ?
? 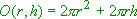
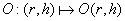 zu einer Funktion
zu einer Funktion 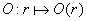 umformen?
umformen? 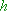 mit Hilfe des vorgegebenen Volumens her.
mit Hilfe des vorgegebenen Volumens her. 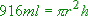
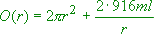 .
.