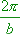Um die grundlegenden Eigenschaften der Sinusfunktion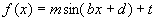 
(
, 
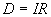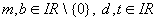) zu untersuchen, wird diese auf die Form 
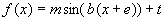mit 
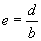gebracht.
- Falls du schon in GeoGebra etwas verändert hast, stelle rechts oben mit dem
-Logo die Ausgangsposition wieder her.
Ziehe nun mit der Maus am Schieberegler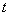
und beobachte wie sich der Graph verhält! 
Schaue besonders auf den Wert von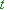 
im Zusammenhang mit der Verschiebung der Sinuskurve entlang der y-Achse.
Was gibt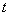 also an?
Notiere deine Behauptung möglichst (mathematisch) exakt!
Die Sinuskurve wird um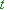 in Richtung der y-Achse verschoben.
- Setze jetzt als Erstes den Wert von 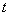wieder auf
.
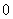Bewege den Schieberegler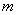
und schaue wie sich der Graph verhält. Vergleiche mit der schwach eingezeichneten Sinuskurve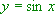 
.
Was kann an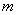 abgelesen werden?
(Fallunterscheidung)
An
kann Folgendes abgelesen werden:
-
: gibt die Amplitude an
-
: Streckung des Graphen in Richtung der y-Achse.
-
: Stauchung des Graphen in Richtung der y-Achse.
-
: Zusätzliche Spiegelung von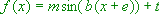 
(
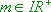) an der x-Achse.
- Schiebe zunächst 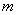zurück auf 1.
Ziehe nun am Schieberegler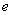
und beobachte die Sinuskurve. Vergleiche mit der schwach eingezeichneten Sinuskurve .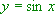
Was gibt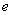 also an?
Durch diesen Parameter wird die Verschiebung der Sinuskurve um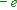
entlang der x-Achse angegeben.
- Stelle den Wert von 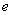wieder auf 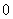ein.
Bewege den Schieberegler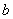
und beobachte wie sich der Graph verhält. Schaue besonders auf die Periode der Kurve.
Was ist an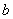 alles ablesbar? (Fallunterscheidung)
An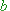
kann Folgendes abgelesen werden:
-
: Stauchung des Graphen in Richtung der x-Achse.
-
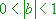: Streckung des Graphen in Richtung der x-Achse.
-
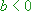: Zusätzliche Spiegelung von (
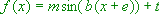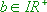) an der x-Achse, denn es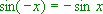 gilt: 
Bei der Kosinusfunktion gilt: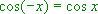 
.
- Zusatzinformation: Periode:
