Lösungshinweise:

Allgemeiner Hinweis:
Wenn Sie am Punkt Hilfe ziehen, dann werden Fasskreisbögen über [AB] zu den Winkeln 10, 20, 30, , 170 eingezeichnet.

1. γ > α
• Die Längen der Strecken [AB] und [BC] sind konstant und die Strecke [AB] ist länger als die Strecke [BC].
• Da der größeren Seite der größere Winkel gegenüberliegt, folgt γ > α.

 

2. γ = α
• Wenn C mit P zusammen fällt, dann gilt γ = 180 und α =0, es folgt also weiterhin γ > α.
• Wenn allerdings C mit Q zusammenfällt, dann gilt γ = 0 und α =0, also folgt γ = α.

 

3. Wie ändert sich α?
• α wird zunächst sehr schnell größer, da die Bewegung nahezu senkrecht zum 2. Schenkel erfolgt und dann langsamer, da die Bewegung immer mehr in Richtung des 2. Schenkels erfolgt..
• Maximum:
  AC ist Tangente an den Kreis (γ = 90).
  Begründung:
  1. AC ist Sekante (C ist erster / linker Schnittpunkt).
  2. AC ist Tangente (C ist Berührpunkt).
  3. AC ist Sekante (C ist zweiter / rechter Schnittpunkt).
  Der erste Schnittpunkt bewegt sich wieder auf den Punkt P zu. Da der Weg von C (dem zweiten Schnittpunkt) aber nun deutlich länger ist, wird α deutlich langsamer kleiner als er vorher gewachsen ist.

   

4. Wie ändert sich γ?
• C = P:   γ = 180.
• C = Q:   γ = 0.
• Dazwischen wird γ kleiner, da immer neue Fasskreisbögen geschnitten werden. (Ziehen Sie zur Anzeige der Fasskreisbögen bitte am Punkt "Hilfe".) Die Änderung erfolgt zunächst relativ schnell, da die Fasskreisbögen relativ dicht beieinander liegen, und wird dann geringer.

 

5. Wie ändert sich der Graph von α(β)?
   • A Þ P:
     Der Berührpunkt der Tangente wandert auf P zu.
     Þ Das Maximum verschiebt sich nach links und wird größer.
   • A = P:
     Das ΔABC ist gleichschenklig.
     Þ γ = α. Die beiden Winkelgrößen nehmen linear von 90 beginnend (C = P) bis zu 0 (C = Q) ab.
   • P A B:
     1. C = P:   α = 180.
     2. C = Q:   α = 0.
     3. Dazwischen wird α immer kleiner, zuerst relativ schnell, da die Bewegung fast senkrecht zum zweiten Schenkel erfolgt, dann langsamer.
   • A = B:
     αist Nebenwinkel von β. Da β linear von 0 auf 180 anwächst, nimmt αlinear von 180 auf 0 ab.

    

6. Wie ändert sich der Graph von γ(β)?
   • A Þ P:
     Am Anfang immer steiler, da die Fasskreisbögen immer enger beieinander liegen, am Ende immer flacher, da die Fasskreisbögen immer weiter auseinander liegen.
   • A = P:
     Das ΔABC ist gleichschenklig. Þ γ = α. Die beiden Winkelgrößen nehmen linear von 90 beginnend (C = P) bis zu 0 (C = Q) ab.
   • P A B:
     γ hat ein Maximum, da einer der Fasskreisbögen, den Kreis
      
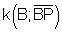
     berührt. In der Umgebung des Maximums ist die Änderung gering, da C sich annähernd auf einer Tangente an den Berührfasskreisbogen bewegt.
   • A = B:
     Die beiden Schenkel von γfallen zusammen, d. h. es gilt: γ = 0.